力学⑤ 慣性モーメントの応用

慣性モーメントによる運動方程式
慣性モーメントを用いると、回転に関する運動方程式が簡単に記述できます。力のモーメントの定義
慣性モーメントを用いた角度方向の運動方程式
\begin{align*}I\dfrac{d^{2}\boldsymbol{\theta}}{dt}=I\dfrac{d\boldsymbol{\omega}}{dt}=\boldsymbol{N}=\boldsymbol{r\times F}\end{align*}
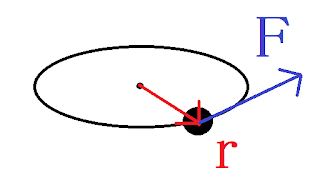
ただし、$\boldsymbol{r}$は位置を表すベクトル、$\boldsymbol{F}$は外力、$\boldsymbol{N}$は力のモーメント(トルク)です。
力のモーメントの数学的な定義
また、力のモーメントの定義は外積によって定義されています。 これを言葉で説明すれば、力のベクトルを位置を表すベクトル$\boldsymbol{r}$に垂直な成分と平行な成分に分解し、垂直な成分と軸との距離との積を取っています。 念押しですが、外積の計算結果はベクトルになるので、力のモーメントはベクトル量です。ベクトルの向きは図では上向きです。外積の向きというのは、右ねじの考え方を使って考えるのでした。だから$\boldsymbol{r\times F}$とモーメントを定義すれば、上向きにモーメントが向きます。
角運動量の定義
角運動量
\begin{align*}\boldsymbol{l=r\times p}\end{align*}
ただし、$\boldsymbol{r}$は位置を表すベクトルで、$\boldsymbol{p}$は運動量です。この式をすこしいじってみると以下のような式が導出できます。
角運動量と力のモーメントの関係
\begin{align*}
\dfrac{d\boldsymbol{l}}{dt}=\boldsymbol{N}
\end{align*}
\begin{align*}
\dfrac{d\boldsymbol{l}}{dt}=\dfrac{d\boldsymbol{r}}{dt}\times \boldsymbol{p}+\boldsymbol{r}\times \dfrac{d\boldsymbol{p}}{dt}
\end{align*}
となります。ここで、第一項について、運動量ベクトルは速度ベクトルにスカラーである質量をかけただけ、つまり
\begin{align*}
\boldsymbol{p}=m\dfrac{d\boldsymbol{r}}{dt}
\end{align*}
になります。つまり、運動量ベクトルと速度ベクトルは平行といえるでしょう。平行なベクトルの外積は零ベクトルになるので、第一項は$\boldsymbol{0}$になります。また、第二項について、Newtonの運動方程式より、
\begin{align*}
m\dfrac{d\boldsymbol{r}}{dt}=\dfrac{d\boldsymbol{p}}{dt}=\boldsymbol{F}
\end{align*}
となることを利用すれば、
\begin{align*}
\dfrac{d\boldsymbol{l}}{dt}=\boldsymbol{r}\times \boldsymbol{F}
\end{align*}
さて、この左辺は力のモーメント$\boldsymbol{N}$になります。慣性モーメントとモーメント、角運動量の関係
$z$軸周りの慣性モーメントは以下のように定義されました。\begin{align*}
I=\sum_{(x,y)}\Delta m(x,y)(x^2+y^2)
\end{align*}
以下、回転軸を$z$軸として考えましょう。
質点で考えてみる
一旦、話が簡単な質点で考えてみることにしましょう。半径$r$の円周上を質量$m$の質点が回転している状況を考えましょう。つまり、慣性モーメントは以下のようになります。\begin{align*}
I=mr^2
\end{align*}
円筒座標をとる
円筒座標をというものを導入して計算します。3次元では、$z$軸はそのままで、$x,y$軸を半径方向の$\boldsymbol{e_r}$と、回転方向$\boldsymbol{e_\phi}$に分けた座標を取ります。$\boldsymbol{e_\phi}$は$z$軸の正の向きから見て反時計回りを正にします。ここで、$z=0$の平面上、半径$r$の円周に沿って$z$が正の方向からみて反時計周りに大きさ$F$の力を加えたとします。 つまり、$\boldsymbol{r}=r\boldsymbol{e_r},\boldsymbol{F}=F\boldsymbol{e_\phi}$ということです。 このとき、力のモーメントは、$\boldsymbol{N}=(r\boldsymbol{e_r})\times(F\boldsymbol{e_\phi})=rF\boldsymbol{e_z}$で$z$軸の正の方向になります。ここで、運動方程式は、$\boldsymbol{e_\phi}$方向の速度$v$に対して、
\begin{align*}
m\dfrac{dv}{dt}=F
\end{align*}
となります。いま、円周上での運動のみを考えているので、$v=r\omega$と書けるでしょう。よって、さらに辺々に$r$をかけて、
\begin{align*}
mr^2\frac{d\omega}{dt}=rF
\end{align*}
となります。$I=mr^2,N=rF$だったので、
\begin{align*}
I\dfrac{d\omega}{dt}=N
\end{align*}
となります。ただ、このままだとスカラー量になってしまっているので、辺々に$\boldsymbol{e_z}$をつけて、
\begin{align*}
I\dfrac{d\boldsymbol{\omega}}{dt}=\boldsymbol{N}
\end{align*}
$\omega$が回転軸方向に向いていることだけ気を付けてください。今回は$z$軸方向に向いています。ここで、$\boldsymbol{\omega}=\dfrac{d\boldsymbol{\theta}}{dt}$とおくと、
\begin{align*}
I\dfrac{d^2\boldsymbol{\theta}}{dt^2}=I\dfrac{d\boldsymbol{\omega}}{dt}=\boldsymbol{N}
\end{align*}
とできます。これで最初に示した回転運動に関する運動方程式が特殊な場合(質点を考えた場合)ではありますが、示せました。質点の場合を拡張することで一般の場合も考えることができます。
運動エネルギーを慣性モーメントを用いて表す
運動エネルギー
回転運動のエネルギーは
\begin{align*}
\dfrac{1}{2}I\omega^2
\end{align*}
となる。
\begin{align*}
I\dfrac{d\boldsymbol{\omega}}{dt}=\boldsymbol{N}
\end{align*}
の辺々と$\boldsymbol{\omega}$との内積をとると、
\begin{align*}
I\boldsymbol{\omega}\cdot\dfrac{d\boldsymbol{\omega}}{dt}=\boldsymbol{\omega}\cdot\boldsymbol{N}
\end{align*}
ここで、$|\boldsymbol{\omega}|^2=\boldsymbol{\omega}\cdot\boldsymbol{\omega}$の微分を計算します。先ほど外積の微分について積の微分法が使えると説明しましたが、内積についても使えます。しかも、内積は$\boldsymbol{a}\cdot\boldsymbol{b}=\boldsymbol{b}\cdot\boldsymbol{a}$なので、
\begin{align*}
\dfrac{d|\boldsymbol{\omega}|^2}{dt}&=\boldsymbol{\omega}\cdot\dfrac{d\boldsymbol{\omega}}{dt}+\dfrac{d\boldsymbol{\omega}}{dt}\cdot\boldsymbol{\omega} \\
&=2\boldsymbol{\omega}\cdot\dfrac{d\boldsymbol{\omega}}{dt}
\end{align*}
よって、以下の式は時刻で積分すると、$t=t_0$で、$\boldsymbol{\omega}=\boldsymbol{\omega_0}$であり、
\begin{align*}
I\boldsymbol{\omega}\cdot\dfrac{d\boldsymbol{\omega}}{dt}&=\boldsymbol{\omega}\cdot\boldsymbol{N}\\
\dfrac{1}{2}I(|\boldsymbol{\omega}|^2-|\boldsymbol{\omega_0}|^2)&=\int_{t_0}^t \boldsymbol{N}\cdot\boldsymbol{\omega}dt
\end{align*}
ここで、この右辺について、$\boldsymbol{N}=\boldsymbol{r}\times \boldsymbol{F}$でした。先ほど考えていた円周上の質点の運動を考えると、$\boldsymbol{F}=F\boldsymbol{e_\phi}$,$\boldsymbol{r}=r\boldsymbol{e_r}$,$\boldsymbol{\omega}=\omega\boldsymbol{e_z}$なので、
\begin{align*}
\boldsymbol{N}&=(r\boldsymbol{e_r}\times F\boldsymbol{e_\phi})\cdot\omega\boldsymbol{e_z}\\
&=rF\boldsymbol{e_z}\cdot \omega\boldsymbol{e_z}\\
&=r\omega F\\
&=Fv
\end{align*}
よって、
\begin{align*}
\int_{t_0}^t \boldsymbol{N}\cdot\boldsymbol{\omega}dt=Fv(t-t_0)
\end{align*}
右辺は仕事率と時間の積で、加えた仕事を表しています。いま、ポテンシャルの変化はないので、
\begin{align*}
\dfrac{1}{2}I(|\boldsymbol{\omega}|^2-|\boldsymbol{\omega_0}|^2)
\end{align*}
は、運動エネルギーの差を表します。
角運動量の別の定義
先ほど示した\begin{align*}
\dfrac{d\boldsymbol{l}}{dt}=\boldsymbol{N} \\
I\dfrac{d\boldsymbol{\omega}}{dt}=\boldsymbol{N}
\end{align*}
という式をもとに角運動量は以下のように定義されることもあります。
\begin{align*}
\boldsymbol{l}=I\boldsymbol{\omega}=I\dfrac{d\boldsymbol{\theta}}{dt}
\end{align*}
さて、この関係式は運動量の式
\begin{align*}
\boldsymbol{p}=m\boldsymbol{v}=m\dfrac{d\boldsymbol{v}}{dt}
\end{align*}
とすごく似ていますね。ほかにも似たような式を並べておきます。
\begin{align*}
\boldsymbol{l}&=I\boldsymbol{\omega} & \boldsymbol{p}&=M\boldsymbol{v}\\
I\dfrac{d\boldsymbol{\omega}}{dt}&=\boldsymbol{N} & M\dfrac{d\boldsymbol{v}}{dt}&=\boldsymbol{F}\\
I\dfrac{d^2\boldsymbol{\theta}}{dt^2}&=\boldsymbol{N} & M\dfrac{d^2\boldsymbol{x}}{dt^2}&=\boldsymbol{F}\\
K&=\dfrac{1}{2}I\boldsymbol{\omega}^2& K&=\dfrac{1}{2}M\boldsymbol{v}^2
\end{align*}
つまりおおよそ以下の対応を頭に入れておけばよいでしょう。
\begin{align*}
I&\Leftrightarrow M\\
\boldsymbol{\theta}&\Leftrightarrow\boldsymbol{x}\\
\boldsymbol{\omega}&\Leftrightarrow\boldsymbol{v}\\ \boldsymbol{N}&\Leftrightarrow\boldsymbol{F}\\ \boldsymbol{l}&\Leftrightarrow\boldsymbol{p}
\end{align*}