光学② スネルの法則(屈折の法則)
スネルの法則
屈折の法則はスネルの法則ということが多く、フェルマーの原理から導出することができます。屈折の法則
屈折率$n_1$の物質から入社してきた光が屈折率$n_2$の物質との境界面で屈折する状況を考えます。入射角を$\theta_1$、屈折角を$\theta_2$として、以下の法則が成り立ちます。スネルの法則
\begin{align*}
n_1\sin{\theta_1}=n_2\sin{\theta_2}
\end{align*}
フェルマーの原理の式を導出する
フェルマーの原理とは光は以下の$I$を極値をとるような経路をとおるということでした。\begin{align*}
I=\int_{s_1}^{s_2}n(s)ds
\end{align*}
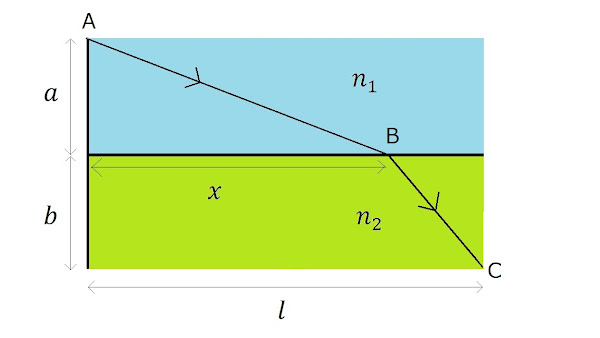
$s$は距離を表すパラメータです。では、以下の画像のような状況を考えましょう。
\begin{align*}
I&=\int_A^Cn(s)ds \\
&=\int_A^Bn_1ds+\int_B^A n_2ds \\
&=n_1\sqrt{x^2+a^2}+n_2\sqrt{(l-x)^2+b^2}
\end{align*}
ここで、$x$の変化に対する作用積分の変化を考えます。仮想的な変位なので変分として$\delta$を使いましたが、実際は微分しているだけです。
\begin{align*}
\dfrac{\delta I}{\delta x}&=n_1\dfrac{2x}{2\sqrt{x^2+a^2}}+n_2\dfrac{2(l-x)\cdot(-1)}{2\sqrt{(l-x)^2+b^2}} \\
&=n_1\dfrac{x}{\sqrt{x^2+a^2}}-n_2\dfrac{l-x}{\sqrt{(l-x)^2+b^2}}
\end{align*}
ここで、フェルマーの原理$\delta I/\delta x$$=0$を課すと、
\begin{align*}
n_1\dfrac{x}{\sqrt{x^2+a^2}}-n_2\dfrac{l-x}{\sqrt{(l-x)^2+b^2}}=0
\end{align*}
となります。ここで、入射角$\theta_1$,屈折角$\theta_2$について、
\begin{align*}
\sin{\theta_1}&=\dfrac{x}{x^2+a^2} \\
\sin{\theta_2}&=\dfrac{l-x}{\sqrt{(l-x)^2+b^2}}
\end{align*}
なので、
\begin{align*}
n_1\sin{\theta_1}-n_2\sin{\theta_2}=0
\end{align*}
となります。これでスネルの法則が導かれました。