微分積分⑤ マクローリン展開・テイラー展開

テイラー展開・マクローリン展開とは?
三角関数や指数関数などの特殊な関数を多項式で表す手法です。ちなみにオイラーの公式(参考:オイラーの公式)を導く手法として使用することができます。また、のちのち多変数関数の話に拡張することもできます。(参考:2変数のテイラー展開・マクローリン展開)
テイラー展開・マクローリン展開の公式
まずは以下のように公式を紹介します。関数を多項式を用いて表すことができます。(ただし,右辺は収束することが条件です。)テイラー展開
以下の式の右辺を$x=a$まわりのテイラー展開といいます。
\begin{align*}
f(x)&=f(a)+\dfrac{1}{1!}f'(a)(x-a)+\dfrac{1}{2!}f''(a)(x-a)^{2}+\cdots\\\
\displaystyle\\ &=\sum_{k=0}^\infty \dfrac{1}{k!}f^{(k)}(a)(x-a)^{k}\end{align*}
マクローリン展開
テイラー展開で$a=0$として
つまり,原点まわりのテイラー展開がマクローリン展開ということです。
\begin{align*}
f(x)&=f(0)+\dfrac{1}{1!}f'(0)x+\dfrac{1}{2!}f''(a)x^{2}+\cdots\\\
\displaystyle\\ &=\sum_{k=0}^\infty \dfrac{1}{k!}f^{(k)}(0)x^{k}\end{align*}
テイラー展開が収束するかどうかというのは、テイラーの定理から評価できます。 (参考:テイラーの定理)
テイラー展開の意味
点$a$まわりのテイラー展開でいえば、$x=a$ですべての微分係数がすべて等しくなるように多項式を設定するのです。たとえば,$n$次までのテイラー展開では、$n$次までの微分係数が等しくなるように多項式を定めます。ただし、$n$次の項の変数部分を点$a$まわりのテイラー展開では$x^{n}$ではなく、$(x-a)^{n}$としている点に注意してください。
テイラー展開による近似手法
テイラー展開をする意味について考えてみましょう。たとえば...$\sin{1°}$ は、いくつでしょう???関数電卓でもないと計算できませんよね。
そこで簡単に計算できる多項式に近似するのです。高校で物理をとっていた人は単振り子の問題などで$x$が小さいときに$\sin {x}≒x$という近似をしたことがあると思います。この近似はマクローリン展開からきています。
テイラー展開の計算方法と剰余項
たとえば$e^{x}$を$x=c$まわりでテイラー展開してみます。この時、$e^{x}$は$x$は$c$に近いから、ほぼ$e^{c}$(=定数)に等しいですね。つまり、
\begin{equation}
e^{x}\approx e^{c}
\end{equation}
でも、これだけだと近似の精度ではあまりよくなさそうですね。
では、一回微分して等しくなるように右辺を設定します。
\begin{equation}
e^{x}\approx e^{c}+e^{c}(x-c)
\end{equation}
確かに、右辺を微分すると左辺と$x$が$c$に近い範囲ではほぼ等しいですね。ここで,点$c$まわりのテイラー展開なので,多項式の部分が$x$ではなく$x-c$にしているのに注意してください。$x=c$としたときに,左辺と右辺が等しくなるように。
もう一回同じことをやってみましょう。左辺と右辺の二階の導関数が等しくなるように,
\begin{equation}
e^{x}\approx e^{c}+e^{c}(x-c)+\dfrac{1}{2}e^{c}(x-c)^{2}
\end{equation}
もう一個、項を増やしてみます。左辺と右辺の三階の導関数が等しくなるようにすると,
\begin{equation}
e^{x}\approx e^{c}+e^{c}(x-c)+\dfrac{1}{2}e^{c}(x-c)^{2}+\dfrac{1}{6}e^{c}(x-c)^{3}
\end{equation}
規則を読み取ってみます。右辺は、整数$n$に対して
\begin{equation}
\dfrac{1}{n!}e^{c}(x-c)^{n}
\end{equation}
の和になっていますね、シグマでまとめれば、$x$が$c$に近いとき
\begin{equation}
\displaystyle \sum_{k=0}^\infty \dfrac{1}{n!}e^{c}(x-c)^{n}
\end{equation}
と表せます。たとえば、$e^{c}$が具体的に計算できるのは$c=0$ぐらいなので、$c=0$としてみます(つまり、マクローリン展開)
\begin{equation}
\displaystyle e^{x}=\sum_{n=0}^\infty \dfrac{1}{n!}x^{n}
\end{equation}
こんな風に多項式で書けました。
$n$が大きい項は影響が小さいので、手計算ではある程度の$n$で止めておくのが現実的です。そこで,たとえば2次の項まで計算したことを示すために,
\begin{equation}
f(x)= f(0)+f^\prime(0)x+\dfrac{1}{2}f^{\prime\prime}(0)x^2+O(x^3)
\end{equation}
などと書きます。この最後の項が剰余項です。いろいろな書き方がありますが、今回用いたのはランダウの記号です。
ランダウの記号(Landau)が表すことは?
ランダウの記号には二種類あります。大きいオミクロンと小さいオミクロンです。ざっくりいうと,\begin{align*}
f(x)=O(g(x))&\Leftrightarrow \lim_{x\to a} \frac{f(x)}{g(x)}=\text{0以外の定数}\\
f(x)=o(g(x))&\Leftrightarrow \lim_{x\to a} \frac{f(x)}{g(x)}=0
\end{align*}
この二つです。マクローリン展開では、$a=0$として考えます。たとえば,$f(x)=x^4+3x^3$は,$O(x^3)$,または,$o(x^2)$です。もしくはもっと粗く$o(x)$と表記しても構いません。小さいオミクロンだといくらでも大きい次数で押さえつけられてしまって,どれくらいの精度かわからなくなるので,大きいオミクロンのほうが好まれます。
近似できる範囲
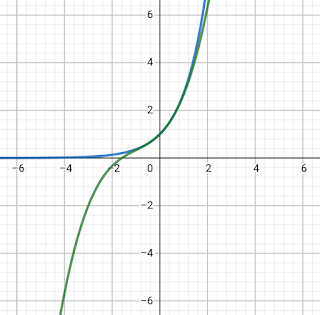
仮定で言ってありましたが、あくまで$x=c$のまわりにテイラー展開したなら、$x=c$に近い$x$ではないと成り立たないことが多くあります。下のグラフは$e^{x}$のグラフ(青)とその3次までのマクローリン展開(緑)を比較したグラフです。すなわち、\begin{align*}
\text{青}:y&=e^{x}\\
\text{緑}:y&=1+x+\dfrac{1}{2}x^{2}+\dfrac{1}{6}x^{3}
\end{align*}
$x=0$の近くでは確かにいい近似だけど離れるとあんまり…って感じですね。というわけで有限時までの近似には限界があります。