ベクトル解析⑩ グリーンの定理

グリーンの定理とは?
ここでも、逐次積分の考え方を用います。(参考:逐次積分(ヤコビアンなど))グリーンの定理の使い方と面積
グリーンの定理とは?
グリーンの定理
単純閉曲線(自分と交わらない閉曲線)$C$で囲まれた領域$S$を考えます。$C^1$級の任意の関数$P(x,y)$と$Q(x,y)$について、
\begin{align*}
\oint_{C} (Pdx+Qdy)=\iint_{S}\left(\dfrac{\partial Q}{\partial x}-\dfrac{\partial P}{\partial y}\right)dxdy
\end{align*}
グリーンの定理の証明
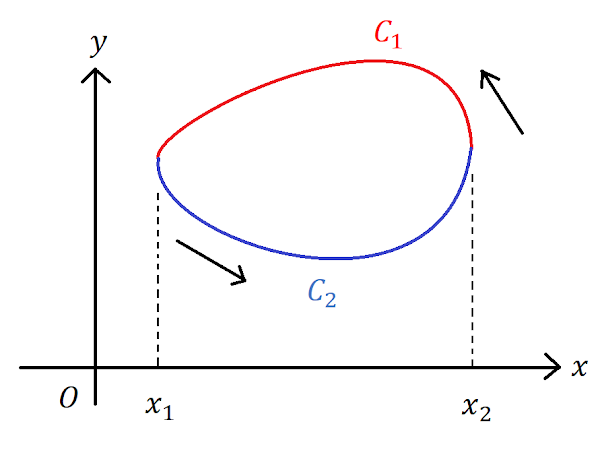
以下のような経路$C$($=C_1+C_2$)を考えます。また、$C$に囲まれた領域を$S$とします。関数Pについての線積分
まず、関数$P$の周回積分を変形することを考えます。ちなみに、$x$と$y$は互いに独立ではないので、片方を動かすと他方もうごくことになります。$x$を動かすことを考えて、$y$を$x$の関数と考えて処理しましょう。$C_1$では$y=y_1(x)$,$C_2$上では$y=y_2(x)$とします。
\begin{align*}
\oint_C P(x,y)dx
&=\int_{C_1}P(x,y_1(x))dx+\int_{C_2}P(x,y_2(x))dx \\
&=\int_{x_2}^{x_1}P(x,y_1(x))dx+\int_{x_1}^{x_2}P(x,y_2(x))dx \\
&=-\int_{x_1}^{x_2}P(x,y_1(x))dx+\int_{x_1}^{x_2}P(x,y_2(x))dx \\
&=\int_{x_1}^{x_2}\left\{P(x,y_2(x))-P(x,y_1(x))\right\}dx \\
&=-\int_{x_1}^{x_2}\left(\int_{y_2(x)}^{y_1(x)}\dfrac{\partial P}{\partial y}dy\right)dx \\
&=-\int_S \dfrac{\partial P}{\partial y}dxdy
\end{align*}
関数Qについての線積分
$Q$は$y$についての線積分なので、$y$に注目して動かします。つまり、$x$を$y$の関数として、考えて同様の計算で進めます。たとえば、右半分の経路を$x_2(y)$,左半分の経路を$x_1(y)$として計算します。(ここでは、$y$の最大値を$y_2$,最小値を$y_1$として計算しますが、先ほど使った関数としての文字とは無縁です。)\begin{align*}
\oint_C Q(x,y)dy
&=\int_{y_1}^{y_2}Q(x_2(y),y)dy+\int_{y_2}^{y_1}Q(x_1(y),y)dy \\
&=\int_{y_1}^{y_2}\left\{Q(x_2(y),y)-Q(x_1(y),y)\right\}dy \\
&=\int_{y_1}^{y_2}\left(\int_{x_1(y)}^{x_2(y)}\dfrac{\partial Q}{\partial x}dx\right)dy \\
&=\iint_S \dfrac{\partial Q}{\partial x}dxdy
\end{align*}
領域の面積を線積分で求める
面積を求める公式
単純閉曲線(自分と交わらない閉曲線)$C$で囲まれた領域の面積$S$は
\begin{align*}
S=\dfrac{1}{2}\oint(ydx-xdy)
\end{align*}
\begin{align*}
\oint_{C} (Pdx+Qdy)=\iint_{S}\left(\dfrac{\partial Q}{\partial x}-\dfrac{\partial P}{\partial y}\right)dxdy
\end{align*}
右辺は、面積分ですからその被積分関数が1であれば、右辺は面積となるでしょう。つまり、
\begin{align*}
\dfrac{\partial Q}{\partial x}-\dfrac{\partial P}{\partial y}=1
\end{align*}
ということです。これを満たす$P$,$Q$の選び方は一通りではないですが、簡単な形であること、対称的なことを考えれば、
\begin{align*}
P(x,y)&=-\dfrac{1}{2}y \\
Q(x,y)&=\dfrac{1}{2}x
\end{align*}
となります。このとき、グリーンの定理から、
\begin{align*}
S=\iint_S dxdy=\dfrac{1}{2}\oint (ydx-xdy)
\end{align*}
と、面積を求める公式が導かれました。