力学③ 仕事の線積分による計算・保存力の判定方法
仕事の計算と保存力・ナブラの使い方
ナブラの計算と仕事の線積分の計算例あたりをまとめています。運動方程式からエネルギーと運動量を求める
気を付けてほしいのは、運動量はベクトル、エネルギーはスカラー、速度$v$がベクトルです。 その$v$の一次式である運動量はベクトル、二次式(つまり内積で絶対値をとったもの)であるエネルギーはスカラーになります。（1次、とかいう表現はベクトルに対して不適かもしれませんが、こう説明しておきます、考え方です。） 今回も運動方程式から出発しておくと、\begin{align*}
m\dfrac{d^{2}\boldsymbol{x}}{dt^{2}}=m\dfrac{d\boldsymbol{v}}{dt}=\boldsymbol{F}\ \therefore m\ d\boldsymbol{v}=\boldsymbol{F}\ dt
\end{align*}
この式の左辺が運動量$\boldsymbol{p}$の微小変化です。
この辺々と$\boldsymbol{v}$の内積を取って、辺々を積分します。$t=0$で初速度$\boldsymbol{v_0}$，初期位置$\boldsymbol{x_0}$として計算します。積分の変数には積分範囲を表す文字と区別するためにプライムをつけています。
\begin{align*}
\dfrac{1}{2}m\boldsymbol{v}^{2}-\dfrac{1}{2}m\boldsymbol{v_0}^2=\displaystyle \int_0^t \boldsymbol{F}・\boldsymbol{v}dt^\prime =\int_{\boldsymbol{x_0}}^{\boldsymbol{x}} \boldsymbol{F}・ d\boldsymbol{x^\prime}
\end{align*}
ここで、この右辺は仕事を表しています。
つまり、もし，初速度が$\boldsymbol{v_0}=\boldsymbol{0}$なら，速さが$v$になるまでに加える仕事を運動エネルギー
\begin{align*}
\dfrac{1}{2}m\boldsymbol{v}^{2}
\end{align*}
としているということです。
ポテンシャルと力の関係とナブラ
次にポテンシャルの話です。いわゆる位置エネルギーのことです。ポテンシャル$Uと力F$のベクトルの関係には、このような関係があります。
ポテンシャルと力の関係
逆三角はナブラと読みます。
ナブラは各成分をそれぞれ偏微分するものです。以下のようにベクトルで表現できます。(参考:ナブラ・ラプラス演算子とは?)
\begin{align*}\boldsymbol{F}=-\nabla U=-\mathrm{grad}\ U=-\left(\begin{array}{x} \dfrac{\partial U}{\partial x}\\ \dfrac{\partial U}{\partial y}\\ \dfrac{\partial U}{\partial y}\end{array}\right)\end{align*}
ナブラ
普通にベクトルだと思って計算すればいいですが，微分演算子なので順番入れ替えはしないようにしましょう。
\begin{align*}
\nabla=\begin{pmatrix}
\dfrac{\partial}{\partial x} \\
\dfrac{\partial}{\partial y} \\
\dfrac{\partial}{\partial z}
\end{pmatrix}
\end{align*}
例：重力の位置エネルギーから重力を導く
$z$軸を鉛直上向きを正にしてとって$U=mgz$というポテンシャルを考えてみましょう。ただの重力の位置エネルギーです。 これを先ほどの式にあてはめれば$z$軸方向の単位ベクトルを用いて$F=-mg\boldsymbol{e_z}$となり重力が導かれます。仕事の定義とは
力$F$がする仕事は線積分で求めます。数学的な線積分の計算方法はベクトル解析の記事で書いています。(参考: 線積分と曲線の長さを求める公式)\begin{align*}
\displaystyle \int_{C} \boldsymbol{F}・d\boldsymbol{r}
\end{align*}
インテグラルの下の$C$は曲線$C$に沿った線積分という意味です。今までは積分経路が$x$軸に沿った積分ばかりを考えていましたが，線積分はその積分経路を好きな曲線に沿うように変えたものです。
$Fとd\boldsymbol{r}$はベクトルです。これは実は$Fとd\boldsymbol{r}$の内積です。
だから本当は点（・）で挟むべきなのでしょうが、略されることも多いです。力の向きが移動する向き(つまり速度の向きと平行または反平行)なら簡単に計算できますが，そうでないときは計算が複雑です...
線積分の計算方法
たとえば，半径$a$の円に沿って反時計回りに一周分動かしたときに大きさ$f$の摩擦力によってなされる仕事を計算しましょう。経路をベクトルで表すと，$0\leq \theta \leq 2\pi$として，\begin{align*}
\boldsymbol{r}=
\begin{pmatrix}
a\cos{\theta} \\
a\sin{\theta} \\
0
\end{pmatrix}
\end{align*}
となります。この辺々を$\theta$で微分すると，
\begin{align*}
\dfrac{d\boldsymbol{r}}{d\theta}=
\begin{pmatrix}
-a\sin{\theta} \\
a\cos{\theta} \\
0
\end{pmatrix}
\end{align*}
となります。ちなみに，摩擦力は運動を妨げる向き，つまり，$\dfrac{d\boldsymbol{r}}{d\theta}$と逆向きにはたらくので，
\begin{align*}
\boldsymbol{F}=
\begin{pmatrix}
f\sin{\theta} \\
-f\cos{\theta} \\
0
\end{pmatrix}
\end{align*}
これをもとに線積分を計算すると，
\begin{align*}
\int_C \boldsymbol{F}\cdot d\boldsymbol{r}
&=\int_0^{2\pi} \boldsymbol{F}\cdot \dfrac{d\boldsymbol{r}}{d\theta}d\theta \\
&=\int_0^{2\pi}
\begin{pmatrix}
f\sin{\theta} \\
-f\cos{\theta} \\
0
\end{pmatrix}
\cdot
\begin{pmatrix}
-a\sin{\theta} \\
a\cos{\theta} \\
0
\end{pmatrix}
d\theta \\
&=-\int_0^{2\pi} fa(\sin^2{\theta}+\cos^2{\theta})\ d\theta \\
&=-\int_0^{2\pi} fa\ d\theta\\
&=-2\pi fa
\end{align*}
保存力の判定方法・回転
保存力は元の位置に戻ってきたときに仕事の総和が0になるような力のことです。たとえば、重力とか。 逆に保存力でないものは、摩擦力などがあります。 ここで重要なのは、保存力かどうかの判定です。なぜこれで保存力が判定できるのかは後で説明するので，とりあえず条件だけ納得してください。
保存力であるための条件
であることです。
ベクトルどうしが「$\times$」という演算で結ばれていますが、これは外積です。
\begin{align*}
\nabla\times \boldsymbol{F}=\mathrm{rot}\ F=\boldsymbol{0}\end{align*}
\begin{align*}
\boldsymbol{a}\times \boldsymbol{b}=\left(\begin{array}{b}a_{y}b_{z}-a_{z}b_{y}\\ a_{z}b_{x}-a_{x}b_{z}\\ a_{x}b_{y}-b_{y}a_{x}\end{array}\right)
\end{align*}
すなわち、
\begin{align*}
\nabla \times \boldsymbol{F}=\left(\begin{array}{b}\dfrac{\partial F_{z}}{\partial y}-\dfrac{\partial F_{y}}{\partial z}\\ \dfrac{\partial F_{x}}{\partial z}-\dfrac{\partial F_{z}}{\partial x}\\ \dfrac{\partial F_{y}}{\partial x}-\dfrac{\partial F_{x}}{\partial y}\end{array}\right)
\end{align*}
覚え方としては例えば、私は、$x$成分について、$x$成分以外の2文字、$y,z$に着目します。$x\to y\to z$の順に着目した文字で偏微分することを考えます。今回の場合、$y,z$に着目しているので$y$で偏微分して,$z$で偏微分するという感じに覚えています。
(覚え方はまあ人それぞれですから覚えられればそれでOKです)
ストークスの定理から保存力を判定する
ちなみに... なんでこんな式で判定できるのか、ということについてです。 （直感的ではなく数学的な説明になってしまいますが...） ベクトル解析の公式にストークスの定理があります。(参考:ストークスの定理)
ストークスの定理(Stokes)
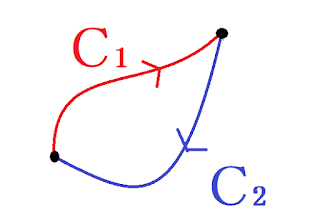
こんな線に沿って積分することを考えてみましょう。
\begin{align*}\displaystyle \iint_{S} \mathrm{rot}\ \boldsymbol{F・n}dS=\oint_{C_{1}+C_{2}}\boldsymbol{F}・d\boldsymbol{r}\end{align*}
